The Browser You Loved to Hate

I didn't plan on giving Microsoft so much free attention by posting their videos, but this one is fascinating.  It has a computer geek in therapy admitting he used to uninstall Internet Explorer from everyone's computer, but he's over it now "because IE9 is actually good."

Best line:  "The only thing Internet Explorer is good for is downloading other browsers."

Unlike the other Microsoft videos I have posted, this one doesn't target Google specifically, but Microsoft is clearly wary of the browser competition that is slowly eating away its market dominance.  Depending on which browser usage statistics you prefer (here is one version), IE is steadily losing ground and Google Chrome is close to overtaking Firefox as IE's main competition.

Admitting your product used to be awful is a risky move, but honesty could actually work.  That is, if the new IE9 browser is actually as good as they say it is.  My experience says it's not.

I use IE9 at my client's location specifically to access Sharepoint and Outlook Webmail.  Sharepoint works better in IE9 than in Chrome, but Webmail is glitchy in IE9.  (The delete email icon generates an error more than half the time, and it hangs occasionally when trying to send an email.)  Strangely enough, Webmail is not glitchy in Chrome.  If I were Microsoft making both IE9 and Outlook Webmail, you'd think I would intentionally make Webmail work best in IE9.  Alas, not so.

This leads me to believe that Microsoft will be able to recycle this same ad campaign for IE10 too.

Microsoft's New Video Mocking Google

Last year I posted a video from Microsoft mocking Google's Gmail.  The Gmail-man clip was funny and well-written, if not completely accurate in the information it conveyed.  I thought it was a good jab at the competition.

Now Microsoft has a new video mocking Google Documents, called "Googlighting."  Unfortunately this one is not funny, just desperate.  It's obvious that Microsoft sees Google as a threat to its own Office 365 cloud services.

When Data Mining Makes You Smart, Should You Play Dumb?

If your data mining tools are successful at giving you business intelligence about your customers, should you act like you have that intelligence?  Or should you play dumb?

I started thinking about this after reading an article in this weekend's NY Times called "How Companies Learn Your Secrets" by Charles Duhigg.

The article describes how Target stores have had success at mining their customer data to figure out which customers are likely expecting a baby.  In fact, they even go as far as predicting the due date.  It turns out people change their buying habits during periods of major change in their lives, and having a baby is about the biggest life change that comes around.  However, if you wait until after the baby is born, you are already too late.  The changes in buying habits have already occurred.  Target tried to influence those buying habits during the second trimester of a pregnancy.

And they were good at it.  Too good in fact.  When women got coupon books with coupons for pregnancy and baby needs, they got spooked.  Their response was, "How did Target know I was expecting when I haven't told them?"  They wouldn't use the coupons.

So Target dumbed things down a bit.  Instead of sending customized flyers with just baby products, they added random coupons for things the expectant mother would not be interested in, such as a lawn mower.  When the woman thought she was getting the same flyer as every other house on the block, she would gladly use the baby coupons.

It seems like business intelligence is becoming more like its namesake, military intelligence.  When you know something about your adversary, it is only helpful to you if they don't know that you know it!  When the British broke the German Enigma code, they obviously wanted to use it in their war efforts, but they were also careful not to demonstrate their knowledge to the Germans.  That meant sometimes you didn't use that intelligence.  The most famous instance (still debated about its truthfulness) was when Churchill knew Coventry was to be bombed based on Enigma intercepts, but did not take defensive measures which would tip off the Germans.

Now that we are achieving some success at business intelligence, we have a new decision to make:  When do we choose to NOT use our knowledge about our customers in order to keep them buying from us?

Medians, Distributions, and Cancer Statistics

I found a fascinating essay archived  on cancerguide.org by evolutionary biologist Stephen Jay Gould entitled, "The Median Isn't The Message."  It's a story about how cold, stark cancer statistics became intensely personal after Gould was diagnosed with a rare form of cancer in 1982.

Having spent years myself as a data jockey in the healthcare system, including in a cancer agency, I am familiar with those cold statistics.  I had many of them memorized for easy retrieval.  Whenever I heard about an acquaintance who had been diagnosed with cancer, I would immediately determine in my head the likelihood of treatment success.  It was not the kind of information that was particularly helpful to the patient, and I quickly learned to keep that information inside my head!

Gould's cancer had a median survival of 8 months from diagnosis -- not very good odds at all.  Half of these cancer patients survived LESS than 8 months!  Being a biologist familiar with statistics, he forced himself away from the reflex conclusion that he had about 8 months to live.  The important information was the shape of the survival distribution curve, not in the median value.

As with most healthcare distributions, cancer survival is an exponential curve with a long tail to the right, meaning a few people survive much longer than the median.  The second consideration was to determine what factors classified those patients into subgroups within that distribution.  Age was one, and since Gould was relatively young, his odds at beating the median survival were better than average.

In Gould's case, a new experimental treatment turned out to separate him from the rest of the distribution and he survived for another 20 years.  When he died in 2002, it was from an apparently unrelated form of cancer.

The main point of the article is to always understand your data before you draw conclusions from it, and the best way to understand data is to look at it visually.  I always told my analysts to start with a graph of the dataset and then focus the analysis on the interesting parts.  Simply starting with averages, medians, minimums, maximums, and even fancy statistical measures like correlation coefficients will not tell you enough.

That's where Business Intelligence and Data Mining tools really make life easy.    Visualizing the data will convey much more useful information than a table of statistics.  In BI, a picture is definitely worth a thousand words!

Statistician Francis Anscombe demonstrated this principle elegantly in 1973 by creating four datasets with very different distribution shapes, but almost identical statistical properties.  They are known as Anscombe's Quartet. 

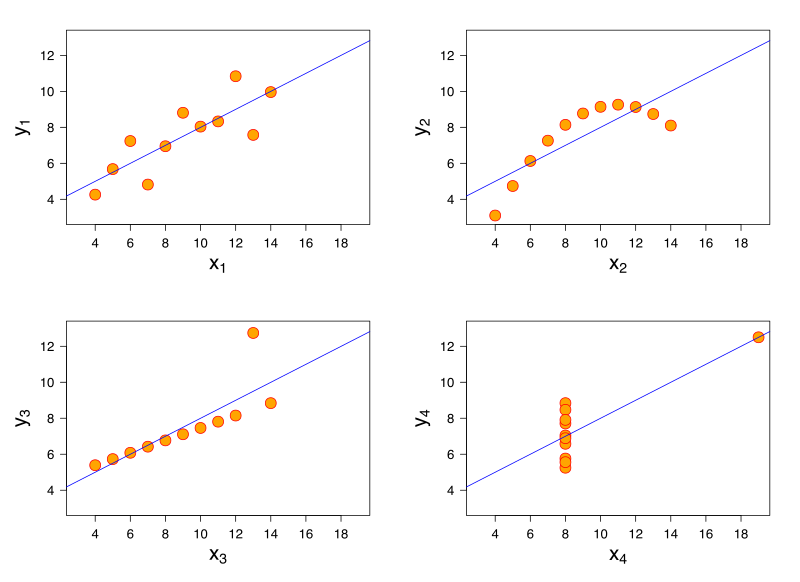
The datasets all have the same average values for x, same average values for y, and the same variances for each.  In a normal or bell curve distribution, you can think of the variance as a measure of the width of the bell.  In a cluster of data points, variance can be understood as average minimum distance from the best-fit line running through them.  The Anscombe datasets also have the same linear regression result (i.e. the best-fit line through the data points) and the same correlation values.  Correlation is a measure of how much the x- and y-values move together.  A high positive correlation means that when x increases, so does y.

In Anscombe's Quartet, the first dataset is a textbook example of how these statistical functions are supposed to work.  The variance, regression line, and correlation are all accurate descriptions of the behaviour of this group of data points.

However, the third dataset is skewed by a single outlier.  The slope of the regression line is off, and the correlation should be a perfect 1 if the outlier is excluded.   Graphing the data makes outliers very obvious.  Sometimes outliers are measurement errors and should be excluded, but if there are many outliers it suggests there are two different datasets being displayed together.

The second dataset shows the bias of incomplete measurement.  The data is clearly curving, so a linear regression is arbitrary in that it would differ greatly if we made one more measurement, and it would differ again if we made two more measurements.  The x- and y-values are related to each other, but in a completely non-linear way.  Regression should not be considered in this case as it is meaningless.

The fourth dataset shows a completely uncorrelated, non-linear dataset with a single outlier, yet the statistical measures still generate the same results as the first dataset suggesting a high degree of correlation and linearity.  This is a stellar example of how statistical measures can be completely erroneous if used blindly.

The Anscombe Quartet highlights the frailty of some statistical measures when you leave the realm of linear or normal distributions.  Bell curves are nice, but they don't exist everywhere in the real world.  If you assume bell curves or linear relationships without verifying them first, your analytical conclusions will be way off base.

Margin, Efficiency, and the DuPont Formula - Part 2

In Part 1, I reviewed 8 companies with a wide range in both margins and profitability and showed that high margins do not always translate into high profits.  The explanation for these profitability variations lies somewhere other than with margin.  However, comparing different companies is challenging.  There are many aspects that must be considered.  That's where the DuPont Formula can be helpful.

Developed in the 1920's by the chemical company DuPont, it takes the Return on Equity ratio and expands it.  It attempts to answer why company A's Return on Equity (ROE) is different than company B's.

Return on Equity is simply profit divided by shareholders' equity, where equity is the value of the company as measured by its assets (what it owns) minus its liabilities (what it owes).  ROE is a measure of how efficient a company is at generating profits from its investors' equity.

Looking at two of the companies from Part 1, Rogers has an ROE of 38.6% but Bell's ROE is less than half that at 15.0%.  At first glance this is surprising, given they are both in the same industry, have similar margins, and have similar net income per share.  Why should their ROE be so different?

The DuPont Formula, Step 1

The DuPont formula expands the ROE ratio into 3 parts.

The first ratio in this expanded equation is simply the profit margin, or the margin when all types of expenses are included.  In Part 1, we only looked at Operating Margins.  It turns out the net Profit Margins for Rogers and Bell are also similar (12.5% and 12.0% respectively).

Asset turnover is the rate at which the company's assets generate sales, which is really the only reason for having assets.  A turnover of 1 means the assets generate an equal amount of sales every year. 

The equity multiplier is a measure of financial leverage, or the amount of debt being used by the company.  Assets can be purchased either by using shareholder equity or by using loans.  Because Assets = Liabilities + Equity, a higher proportion of loans (i.e. liabilities) means a lower proportion of equity, and therefore a higher ROE.

Plugging the numbers into the formula, we get the following:

Company	ROE	Profit Margin	Asset Turnover	Equity Multiplier
Rogers	38.6%	12.5%	0.70	4.38
Bell	15.0%	12.0%	0.46	2.72

It is clear that while Rogers and Bell are similar in profit margin, they are very different in asset turnover and leverage.  Rogers generates a much higher rate of sales given its assets, and it also uses a lot more debt relative to Bell.

The DuPont Formula, Step 2

The formula can be expanded further, providing more information about the profit margin ratio.  Instead of 3 separate component ratios, there are now 5.

The profit margin is now split into 3 components of its own.

Net Profit over Pretax Profit measures the company's tax burden, typically something that the company has very little control over.  It is dependent on the jurisdiction that it operates in, and other regulatory costs that governments sometimes impose on certain industries.

Pretax Profit over  Earnings Before Interest and Taxes (EBIT)  is the interest burden, a measure of both the amount of debt and the interest rates the company is charged.  This is largely within control of the company, and it is related to the leverage ratio.  While more debt potentially increases return on equity by permitting the purchase of additional assets, it also increases the interest burden which in turn lowers return on equity.

Finally, EBIT over Sales is a measure of the ability of the company to generate earnings, including non-operating revenues, given the amount of sales they have.

Plugging in these numbers, we get the following:

Company	ROE	Tax Burden	Interest Burden	EBIT/ Sales	Asset Turnover	Equity Multiplier
Rogers	38.6%	0.71	0.76	23.0%	0.70	4.38
Bell	15.0%	0.80	0.80	18.7%	0.46	2.72

In the first table, Rogers and Bell had similar profit margins (12.5% and 12.0% respectively), with Rogers being slightly better.  Now that measure is shown as three components, we can see that Rogers' lead is not due to lower taxes (they pay slightly more than Bell as a ratio) and it's not due to lower interest payments (they pay more than Bell), but it's due to their better ability to generate earnings relative to their sales.

The DuPont Formula has taken that single ROE measure and split it into five different components that tell a much more detailed story about these two similar companies.